Week 3: Julia言語入門１

今日やること

アイスブレイク

まず教員・TA・ゲストのAWSの方々が自己紹介をします。次に、受講生の方々に自己紹介をしていただきます。以下は成績などに一切考慮しないので、自由に意見を述べてください。

• 苗字の五十音順に自己紹介をしてください。

  • まず一人で発言内容を考えてください（1分）

  • 自己紹介を行ってください。名前、出身地域、出身高校、趣味、入ろうとしているサークル、などなど、言える範囲で大丈夫です。

• 苗字の五十音順に、４人ずつのチームに分けます。以下を議論し、その後順番に発表してください。

  • まず一人で発言内容を考えてください（1分）

  • チームに分かれて議論します（5分）

    • 数週間東大の授業を受けてみた感想はどうでしょうか。簡単？難しい？新しい発見がある？ない？困っていることがある？

    • （この講義は数学に関係するので）特に数学はどんな感じでしょうか？好き？嫌い？

    • これからさらに学びたいことはありますか？

  • チームで発表してください。

• 次に、名前の五十音順に、４人ずつのチームに分けます。以下を議論し、その後順番に発表してください。

  • まず一人で発言内容を考えてください（1分）

  • チームに分かれて議論（5分）

    • 今もってきているパソコンはWindows？マック？その他？

    • 情報系（プログラミング）の経験はありますか？ない？（高校のころの部活や、趣味など？）何か作ったことがあるといった場合は是非紹介してください。

    • 情報系に関して気になっているキーワードはありますか？（AIとか？）

  • チームで発表してください。

連絡用のGoogle Spacesへの招待

教員・TA・学生みなさんの連絡用にGoogle Spacesを用います。Spaceへの招待を行います。

g.eccに関してGmailを開き、左側の「Chat」というところを押すとアクセスできます。「2024初年次ゼミJuliaで学ぶ最適化と機械学習」というSpaceに招待します。

そこでは教員＋TA＋受講生が全員参加しています。気軽にやり取りを行ってください。どんな小さなことでも自由に書き込んでもらってOKです。今後連絡はこのSpaceを使って行います。

AWS SageMaker Studio Labの設定

さて、ここから初期設定を始めます。先ほどの「名前で五十音」のチームに分かれ、以下の設定を行ってください。わからなければチームの人に相談してみましょう。それでもわからなければ、教員・TA・AWSの方々に聞いてみてください。

皆さんには、「AWS SageMaker Studio Lab」というブラウザ環境でプログラミングを実行してもらいます。これは、アマゾンが作っている、ブラウザ上でプログラミングを行うための環境です。通常、プログラミングとは皆さんのノートPC上に様々なものをインストールし、ノートPC上で実行するのが基本なのですが、このSageMaker Studio Labを使うことで、皆さんのパソコンにプログラムをインストールする必要がなくなります。また、皆さんのパソコンのスペックに依存せず、高性能なサーバーでプログラムを実行することができます。今回は、AWS社さんのご厚意により、SagaMaker Studio Labの全面的なパックアップを頂いています。

この環境を使うために、メールアドレスが必要です。メールアドレス以外は何も必要ありません。使うアドレスを決めてください。単に認証のために使うだけなので、普段使いのものならなんでもいいです。大学のものでもいいです。

まず、「リファラルコード」という、お得クーポンコードを配ります。これは黒板に書くので、メモしてください。

次に、以下の手順に従ってAWS SageMaker Studio Labsを設定してください。

• Amazon SageMaker Studio Lab の使い方にアクセスします。

• そのうち、「1. アカウントを作成する」「2. ログインする」「3. Jupyter Labを起動する」まで実行します。

• 以下のような画面になるはずです。

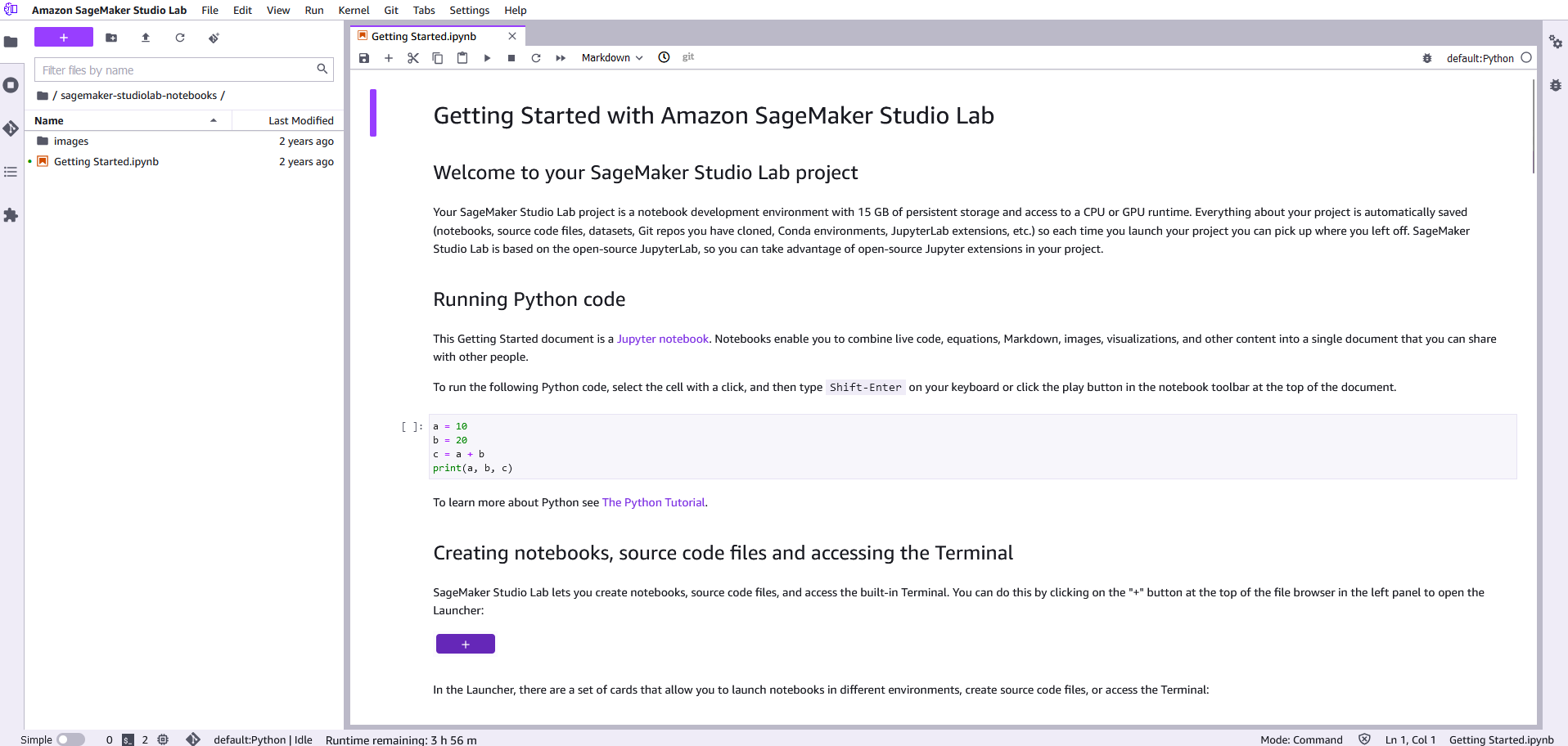
• これで、SageMaker Studio Labの設定は完了です。次に、Juliaをインストールします。

• AWS公式のJuliaインストールスクリプトにアクセスし、真ん中の「Open | Studio Lab」と書いていある紫色のボタンを押す。

• すると、以下のようにこのスクリプトを「SageMaker Studio Lab上で実行していいですか？」と聞かれる画面になります。

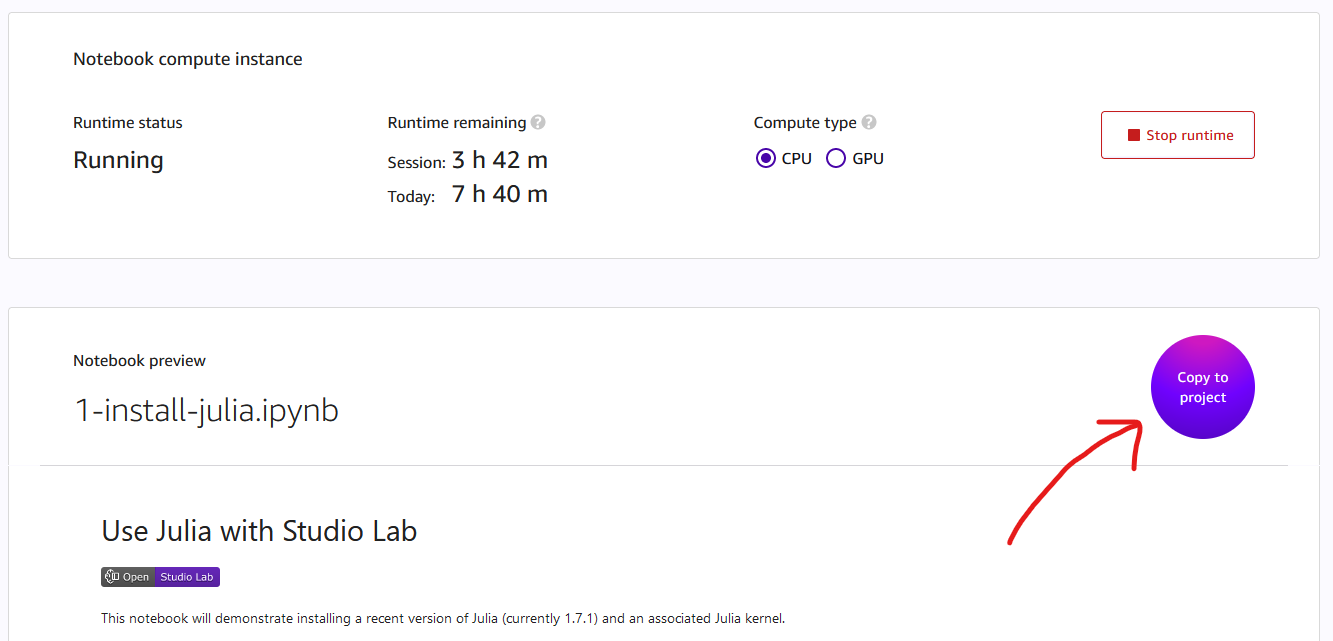
• ここで、「Copy to project」を押します。

• すると、「Copy from GitHub?」と聞かれますので、「Copy Notebook Only」とします。そうすると、先程のスクリプトがSageMaker Studio Lab上にコピーされます。

• そのうえで、%system curl -OL https://julialang-s3.julialang.org/bin/linux/x64/1.10/julia-1.10.2-linux-x86_64.tar.gz などと書かれているブロック（セルと呼ばれます）をクリックし選択したうえで、上部 の「▶」ボタンを押します。これにより、このセルが実行され、Juliaがインストールされます。

• 次に、その直下のセルを選択し、同様に「▶」ボタンを押します。これは必要なものをインストールしていますが、今は気にしないでください。これにはちょっと時間がかかるかもしれません。

• 最後に、その下の２つのセルも同様に実行しておきます。これにてJuliaのインストールが完了です。一度ブラウザをリロードしてみください。

• 左上の「＋」を押したときに、下記のようにJuliaが出てくれば成功です。うまく行かない場合、何度もリロードしてみてください。

• 今後は、ここの「Notebook」「default:Julia (4 threads) 1.10.2」を使い、新しくNotebookを作ってプログラミングを行います。

これにて設定完了です。今後SageMaker Studio Labを実行するにはランディングページをクリックしてください。このリンクはブックマークしておくといいです。

Notebookの使い方

さて、それではこれからプログラミングを行う仕組みを解説します。普通、プログラミングとはmain.jlのようなテキストファイル（メモ帳で作った単なる文字データ）を書き、それをコマンドで実行（julia main.jl）することが基本です。しかし、今回皆さんには、最近流行している「Notebook」という仕組みを使ってもらいます。これは、上記の「ファイルを書く」「実行する」という二段階の処理を合体し、かつそれをブラウザ上で実行可能にすることで、プログラミング作業をよりインタラクティブに実行できるものです。皆さんは２年生や３年生になるとc言語やpython言語を習い通常のプログラミングを勉強することになります。ここでは、その前段階として、Notebookを使ったプログラミングを体験しましょう。

さて、あらためてSagaMaker Studio Labの画面に注目しましょう。ここで左上の「＋」を押し、「Notebook」の「default:Julia (4 threads) 1.10.2」を押してみましょう。次のような画面になります。

ここで、左側はWindowsでいうエクスプローラー、マックでいうFinderのようなものです。たった今新しくNotebookを作ったので、左側にUntitled.ipynbというファイルが見えます。Notebookの拡張子は.ipynbです。出来たばかりのNotebookなのでUntitledという名前になっています。これは自由に変えられます。

このUntitled.ipynbの中身が右側の表示されています。ここでは何も書いていないので、まっさらな状態です。

さて、それでは早速何かを書いてみましょう。右側に四角い領域があると思います。これが「セル」です。ためしにセルの中に

a = 3

と書いてみましょう。ここでは半角英数字を使ってください。このように記載された文章をコードと呼びます。コンピュータは、このようにして記載された文章を実行します。セルの中には自由にコードを書けます。そしてこのセルを実行してみましょう。先ほど上側の「▶」を押すということがありました。これがセルの実行という操作です。「▶」を押してもいいですし、Ctrlキーを押しながらEnterキーを押してもいいです。あるいは、Shiftキーを押しながらEnterでも大丈夫です。すると次のようになります。

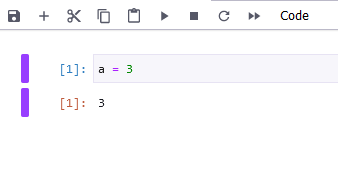
ここでは、セルの直後に、そのセルの実行結果が表示されます。これが、セルの実行です。ここでは、実行したセルの左側に青色で[1]と書かれています。これは、最初に実行されたセルであるという意味の通し番号です。オレンジ色の[1]となっているのは、青い[1]のセルの実行結果という意味です。

さて、セルを追加してみましょう。右側の画面の上部にある「＋」を押すと、セルが追加されます。今度はそこに

3 + 5

と書き、実行してみましょう。次のようになります。

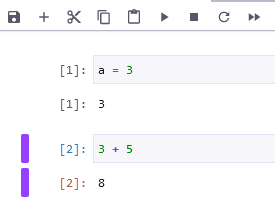
無事足し算が実行できました。このように、セルは自由に追加できます。２度目に実行したので、セルの左側の通し番号は[2]となっていることがわかります。

また、セルをクリックして選択した状態で、上部のハサミアイコンをクリックすると、セルを削除することができます。

セルの実行は、何度でも可能です。セルをクリックし、Ctrl（またはShift）+Enterでいけます。左側の通し番号の[x]がどんどん増えていきます。

また、Notebookはしばしば挙動がおかしくなったり、結果が出ずに固まったりします。その場合、上部の「■」を押して停止させたあと、その右側の 丸い矢印のボタンを押してください。するとNotebookが再起動され、再び実行することが可能になります。ここで、通し番号がリセットされて[1]に戻ることがわかります。 通し番号が振られているうちは、変数などの状態が記憶されているのですが、リセットされるとそれらが消えます。

また、Notebookは実際はファイルなので、Ctrl+sを押すことで保存が可能です。

以上をまとめますと、

• セルを追加したり、セルの中身を編集したりする

• 好きなセルを実行する

• 結果もその場に表示される

というようにして、インタラクティブにプログラミング作業を進めるのが、Notebookです。

Julia言語入門１

さて、それでは基本的な文法を勉強しましょう。来週のWeek4は少し多めにやりますが、その後は毎週少しずつJulia言語について勉強していきます。 今週はとても基本的なことを学びましょう。

先程、以下のような処理を実行しました。

a = 3

ここで、aのようにアルファベットで書かれたものを変数と呼びます。これは、数学の変数に似ている概念です。しばしば「箱」に例えられます。この変数（箱）の中に、値を代入することが出来ます。 変数としてはacbでもhogeでもfuga123でも、なんでも大丈夫です。123abcのように数字から始まるものは許されません。 さて、ここで= 3の部分を見てみましょう。Juliaを始め多くのプログラミング言語では、=は「右辺の値を左辺に代入する」という意味になります。イメージとしては

という感じです。これは、数学の=とは違う意味になります。数学の=はお互いが常に等しいということですが、プログラミングの=は右辺の値を左辺に入れているだけです。試しに、次のように書いてみましょう。

a = 3
a = 5

ちなみに、セルの内部では上記のように改行できます。このセルを実行すると、aの中身が3から5に変わります。これは、最初にaに3を代入した後、aに5を代入したためです。このように、変数は値を上書きすることができます。

ちなみに、ここではNotebookが気を利かせて、セルを実行した際に最後の行を表示してくれるので、画面に「5」と表示されると思います。自分で明示的に表示することもできます。例えば以下のようにしてみましょう。

a = 3
b = 10
println(a)

ここで、println(a)は、「aの中身を表示しろ」という関数です。こうすると、「3」が表示されることがわかります。 上記のように、変数はいくつでも作ることができます。また、あるセルで作り、実行した変数は、他のセルからもアクセスできます。

さて、Juliaは言語レベルでベクトル・行列をサポートしています。例えば次のようにしてみましょう。

x = [1 2 3]

この結果は以下のようになります。

1×3 Matrix{Int64}:
 1  2  3

すなわち、この書き方で1x3の横ベクトルを作ることができました。

同様に、以下のようにして縦ベクトルも作れます。

y = [4;
     5;
     6]

縦ベクトルを作るには、セミコロンを使います。この結果は以下になります。

3-element Vector{Int64}:
 4
 5
 6

無事、縦ベクトルが出来ました。また、セミコロンのあとの空白は無くてもいいため、上記は単純に次のように書いてもいいです。

y = [4; 5; 6]

さて、次に行列です。上記２つの記載方式を組み合わせて、行列を作れます。

A = [7   8  9;
     10 11 12]

この結果は以下になります。

2×3 Matrix{Int64}:
  7   8   9
 10  11  12

また、ここからわかるように、変数名には大文字を使ってもいいです。

要素は小数でも大丈夫です。

B = [1.0 2.0 3.0;
     4.0 5.0 6.0]

この結果は以下になります。

2×3 Matrix{Float64}:
 1.0  2.0  3.0
 4.0  5.0  6.0

ここでは、Int64となっていたものがFloat64になっていることがわかります。これは、数字を表す表現形式が、「64ビットを用いた整数表現」か、「64ビットを用いた小数表現」かを表しています。これらは変数の型と呼ばれます。多くの言語では変数の型を意識することは極めて重要ですが、Juliaはとりあえず気にしなくてもよしなにやってくれるという特徴があります。

さて、行列の足し算・引き算をやってみましょう。あるセルで以下を実行し、2x2の行列を作ってください。

A = [1 2; 3 4]    # セミコロン後の改行を省略。これは2x2の行列

上記のように、「#」以降にはコメントといって、コードを実行する際には無視される、説明文章を付けることが出来ます。

さて、次に別のセルで以下を実行してください。

B = [5 6; 7 8]

ここで、さらに別のセルで以下を実行してみてください。

A + B

以下のような結果になるはずです。

2×2 Matrix{Int64}:
  6   8
 10  12

無事、行列の足し算が行われていることがわかります。

また、a = 3で見たように、結果を別の変数に代入することもできます。例えばベクトルの足し算を以下のようにしてみましょう。

x = [1; 2; 3]
y = x + [6; 7; 8]

ここでは、

3-element Vector{Int64}:
  7
  9
 11

となります。

やってみよう：

• 小数の色々なサイズの行列を作り、足したり引いたりしてみましょう。手計算結果と比較してみてください。

• 行列のサイズが合わないときは、どうなりますか？

• 行列の掛け算もやってみましょう。 A * Bの表記でOKです。これは行列積になります。